NÚMEROS REALES
Unidad 3
Transformar decimal a fracción
a) decimales finitos : son aquellos que tienen fin
b) decimales infinitos periódicos : son aquellos que tiene una o más cifras que se repiten sucesiva e infinitamente , formando el período . Se escribe en forma abreviada coronando al período con un pequeño trazo.
Para transformar un decimal infinito periódico a fracción :
1) Se anota el número y se le resta él o los números que están antes del período (de la rayita)
2) Se coloca como denominador un 9 por cada número que está en el período (si hay un número bajo la rayita se coloca un 9, si hay dos números bajo el período se coloca 99, etc.). Si se puede simplificar, se simplifica.






Reales ℝ
El
conjunto de los números reales pertenece en matemáticas a la recta numérica que
comprende a los números racionales y a los números irracionales. Esto quiere
decir que incluyen a todos los números positivos y negativos, el símbolo cero,
y a los números que no pueden ser expresados mediante fracciones de dos enteros
que tengan como denominador a números no nulos (excluye al denominador cero).
·
Racionales Q: Los números racionales, son
el conjunto de números fraccionarios, números enteros y decimales representados por medio de fracciones. Ejemplo:
2.5
= 25/ 10 = 10/4 = 5/2
8/5
= 1.6
1/7
= 0.142857142857
1/60=0.01666
5/7
o Enteros Z: Es el conjunto formado por los números naturales y sus opuestos, es decir la versión negativa de los números naturales
y el cero. Ejemplo:
Z: ⦋… -3, -2, -1, 0,
1, 2, 3…⦌
o Naturales N: Es el conjunto de números enteros positivos incluyendo el cero. Ejemplo:
N: ⦋0, 1, 2, 3, 4, 5,
6… ⦌
·
Irracionales: Son aquellos
números que no pueden ser representados como una fracción.
Divisor
Que
está contenido en otra cantidad un número exacto de veces. Ejemplo:
5 es divisor de 15, porque 15 lo contiene
3 veces
Múltiplo
Cantidad
que contiene un número exacto de veces a otra cantidad. Ejemplo:
15 es múltiplo de 5, porque 15 lo
contiene 3 veces
Mínimo común múltiplo (m.c.m.)
El
m.c.m.
de un conjunto de números enteros es el menor entero positivo que es el
múltiplo de cada uno de los números dados.
Ejemplo
el m.c.m. de los números 2, 6, 10
4 = 2
6 = (2)(3)
10 = (2)(5)
m.c.m. : (2)(3)(5) = 30.
Máximo Común Divisor (M.C.D.)
El
M.C.D. de un conjunto de números enteros es el mayor entero positivo que es
divisor de cada uno de los números del conjunto .Ejemplo:
El M.C.D. de los números 24, 36, 48:
24 = (23)(3)
36 = (22)(32)
48 = (24)(3)
M.C.D.
: (22)(3) = 12
Ejercicios propuestos
1. Las dimensiones de una caja son: 1,65 m; 2,1 m y 3 m. Se hacen construir cajas cúbicas las mayores que sea posible, cuyo lado sea un número exacto de cm y con las cuales se pueda llenar completamente la caja. Halla el lado y el número de estas cajas.
Pasamos los metros a cm para que sea más fácil el cálculo del mcd
Vamos a hallar el máximo común divisor, haciendo previamente la descomposición en factores.
Vamos a hallar el máximo común divisor, haciendo previamente la descomposición en factores.
300=2351 165=35111 210=23571 =3x5x1=15
Número de cajas: 300 15.165 15.210 15=
20x11x14=3080 cajas
2. Cierto fenómeno tiene lugar cada 450 segundos, otro cada 250, y un tercero cada 600. Si a las 5 de la tarde han coincidido los tres. ¿a qué hora volverán a coincidir por primera vez y cuántas veces tiene lugar cada uno de ellos entre una y otra coincidencia?
Vamos a hallar el mínimo común múltiplo, haciendo previamente la descomposición en factores.
450 = 2351
250 = 251
600 = 2351
= 2351 = 9000
Pasamos los segundos a horas dividiendo por 3600
9000 3600
= 2,5 ℎ
Como coincidieron a las 5 de la tarde, volverán a coincidir a:
5+2,5= 7,5 h; es decir a las 7 y media de la tarde (1930 horas)
¿Cuántas veces tiene lugar cada uno de ellos entre una y otra coincidencia?
9000 450
= 20
9000 250
= 36
9000 600
= 15
3. En un escollo hay 3 faros: uno gira en 2 minutos 12 segundos; otro en 3 minutos 7 segundos; el tercero, en 3 minutos 24 segundos. Lucen juntos a las 12 de la noche. ¿Cuándo volverán a lucir juntos?
Primero pasamos el tiempo de giro de los faros a segundos:
1er faro: 2´12´´= 120´´+12´´= 132´´
2º faro: 3´7´´= 180´´+7´´= 187´´
3er faro: 3´24´´= 180´´+24´´= 204´´
Para calcular cuándo vuelven a lucir juntos, hallamos el mínimo común múltiplo, así:
Así, descomponemos 132, 187 y 204 en factores primos:
132 = 23111
187 = 11171
204 = 23171
168 = 2371
m.c.m. = 231117 = 2244´´
A continuación pasamos los segundos a minutos:
1´ son -----------------------60´´
x´ serán---------------------2244´´
=
2244
60
= 37,4 ´ = 37´24´´
Vuelven a lucir juntos a las 12h 37´24´´
450 = 2351
250 = 251
600 = 2351
= 2351 = 9000
Pasamos los segundos a horas dividiendo por 3600
9000 3600
= 2,5 ℎ
Como coincidieron a las 5 de la tarde, volverán a coincidir a:
5+2,5= 7,5 h; es decir a las 7 y media de la tarde (1930 horas)
¿Cuántas veces tiene lugar cada uno de ellos entre una y otra coincidencia?
9000 450
= 20
9000 250
= 36
9000 600
= 15
3. En un escollo hay 3 faros: uno gira en 2 minutos 12 segundos; otro en 3 minutos 7 segundos; el tercero, en 3 minutos 24 segundos. Lucen juntos a las 12 de la noche. ¿Cuándo volverán a lucir juntos?
Primero pasamos el tiempo de giro de los faros a segundos:
1er faro: 2´12´´= 120´´+12´´= 132´´
2º faro: 3´7´´= 180´´+7´´= 187´´
3er faro: 3´24´´= 180´´+24´´= 204´´
Para calcular cuándo vuelven a lucir juntos, hallamos el mínimo común múltiplo, así:
Así, descomponemos 132, 187 y 204 en factores primos:
132 = 23111
187 = 11171
204 = 23171
168 = 2371
m.c.m. = 231117 = 2244´´
A continuación pasamos los segundos a minutos:
1´ son -----------------------60´´
x´ serán---------------------2244´´
=
2244
60
= 37,4 ´ = 37´24´´
Vuelven a lucir juntos a las 12h 37´24´´
Tipos de Números Decimales
Para
expresar un número racional (a/b) en forma decimal, basta dividir el numerador
por el denominador, obteniendo tres tipos de números Decimales:
- Decimales finitos (0,25; 2,4)
- Decimales infinitos periódicos (0,3333….)
- Decimales infinitos semiperiódicos (2,1666..)
Transformar decimal a fracción
a) decimales finitos : son aquellos que tienen fin
Ejemplos: 4,56 ; 0,0003 ; 2,9876 : 0,1 ; 3,42 , etc.
Para transformar el número decimal a fracción decimal se utilizan potencias de diez (10, 100, 1.000, etc.). Se colocan tantos ceros como cifras decimales tenga el número.
b) decimales infinitos periódicos : son aquellos que tiene una o más cifras que se repiten sucesiva e infinitamente , formando el período . Se escribe en forma abreviada coronando al período con un pequeño trazo.
Para transformar un decimal infinito periódico a fracción :
1) Se anota el número y se le resta él o los números que están antes del período (de la rayita)
2) Se coloca como denominador un 9 por cada número que está en el período (si hay un número bajo la rayita se coloca un 9, si hay dos números bajo el período se coloca 99, etc.). Si se puede simplificar, se simplifica.
c) decimales infinitos semi-periódicos : En estos decimales aparecen una o más cifras antes del período. El número formado por dichas cifras se llama anteperíodo (es un número que está entre la coma y la rayita).
Para transformar un número decimal semi-periódico a fracción:
1) El numerador de la fracción se obtiene , al igual que en el caso anterior, restando al número la parte entera y el anteperíodo, o sea, todo lo que está antes de la “rayita”.
2) El denominador de la fracción se obtiene colocando tantos 9 como cifras tenga el período y tantos 0 como cifras tenga el anteperíodo. Como siempre, el resultado se expresa como fracción irreductible (no se puede simplificar más) o como número mixto.
Leyes de las potencias
Expresiones algebraicas
Una expresión algebraica es una combinación de letras y números ligadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación. Ejemplos:
Ejercicios propuestos:
1) (X + 5/X + 2) + (4X + 5/X + 2)
X + 5 + 4X + 5/ X + 2
5X + 10/X + 2
5(X + 2)/X + 2
5
2) (3/X + 1) – (1/X + 2)
3(X+2) – X – 1/(X + 1)*(X + 2)
2X – 5/X^2 + 3X + 2
3) X^2 – 9/2X + 6
(X + 3) * (X – 3)/2 * (X + 3)
X – 3/2
4) X^2 + 2X + 1/X^2 – 1
(X + 1)^2/(X + 1) * (X – 1)
X + 1/X – 1
Reducir las siguientes expresiones algebraicas
X + 5 + 4X + 5/ X + 2
5X + 10/X + 2
5(X + 2)/X + 2
5
2) (3/X + 1) – (1/X + 2)
3(X+2) – X – 1/(X + 1)*(X + 2)
2X – 5/X^2 + 3X + 2
3) X^2 – 9/2X + 6
(X + 3) * (X – 3)/2 * (X + 3)
X – 3/2
4) X^2 + 2X + 1/X^2 – 1
(X + 1)^2/(X + 1) * (X – 1)
X + 1/X – 1
Reducir las siguientes expresiones algebraicas
1
2 
3
Ecuaciones
Una ecuación es una igualdad matemática entre dos expresiones, denominadas miembros y separadas por el signo igual, en las que aparecen elementos conocidos o datos, desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Ejemplo:
Inecuaciones
Desigualdad entre dos expresiones algebraicas de una o varias incógnitas, que solo se verifica para ciertos valores de esas incógnitas; se expresa con los signos >, <, ≥ y ≤.
Razón y proporción
Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son a y b, la razón entre ellas se escribe como:

Ejercicios propuestos
1. La edad de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.
Solución:
Si las edades son a y b
Cuando nos hablan de relación o razón entre dos cantidades sabemos que nos están hablando de una comparación entre dos cantidades. Por lo tanto expresamos los datos como una razón:
 Ahora volvemos a los datos del problema:
Ahora volvemos a los datos del problema:
Nos indican que la suma de los 2 números nos tiene que dar 84. Esto se expresa así:
 Ahora lo que debemos hacer es trabajar con una constante, que en este caso será " X" . Por lo tanto :
Ahora lo que debemos hacer es trabajar con una constante, que en este caso será " X" . Por lo tanto :
 Reemplazando los datos en la ecuación tenemos:
Reemplazando los datos en la ecuación tenemos:

Ahora que tenemos el valor de x podemos reemplazar para obtener los valores de a y b :
 Respuesta: Por lo tanto podemos decir que las edades son 30 y 54.
Respuesta: Por lo tanto podemos decir que las edades son 30 y 54.
2. El perímetro de un rectángulo mide 128 cm, y la razón entre las medidas de sus lados es 5: 3. Calcula el área del rectángulo.
Solución:
Siguiendo el procedimiento del problema anterior planteamos el problema en una ecuación. Sabemos que el perímetro de un rectángulo es igual a la suma de todos sus lados:
 Si expresamos las variables dadas en el problema:
Si expresamos las variables dadas en el problema:
 Ahora reemplazamos y resolvemos:
Ahora reemplazamos y resolvemos:
 Con este resultado reemplazamos :
Con este resultado reemplazamos :
 Ahora no nos debemos olvidar que nos están pidiendo el área del rectángulo. Sabemos que el área del rectángulos se calcula :
Ahora no nos debemos olvidar que nos están pidiendo el área del rectángulo. Sabemos que el área del rectángulos se calcula :
A = 40 • 24 = 960
Respuesta: El área del rectángulo es 960 cm2
1. La edad de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.
Solución:
Si las edades son a y b
Cuando nos hablan de relación o razón entre dos cantidades sabemos que nos están hablando de una comparación entre dos cantidades. Por lo tanto expresamos los datos como una razón:

Nos indican que la suma de los 2 números nos tiene que dar 84. Esto se expresa así:



Ahora que tenemos el valor de x podemos reemplazar para obtener los valores de a y b :

2. El perímetro de un rectángulo mide 128 cm, y la razón entre las medidas de sus lados es 5: 3. Calcula el área del rectángulo.
Solución:
Siguiendo el procedimiento del problema anterior planteamos el problema en una ecuación. Sabemos que el perímetro de un rectángulo es igual a la suma de todos sus lados:




A = a • b
Por lo tanto la respuesta sería :A = 40 • 24 = 960
Respuesta: El área del rectángulo es 960 cm2



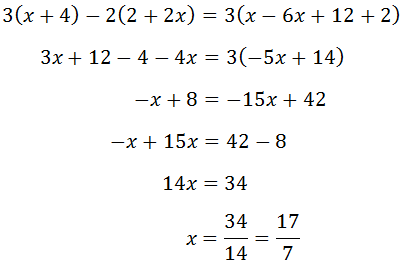
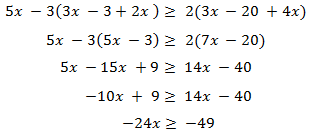
Comentarios
Publicar un comentario